


Next: Spin Precession
Up: Simulations and Systematic Errors
Previous: Gain and Threshold Stability
With our segmented detector, there will on average be much less than
one muon decay recorded in any one channel per measuring period, but
two or more may occasionally come close together in time and this will
happen far more often at the beginning of the interval than at the
end. This situation defines ``pileup.'' When unaccounted for, it
introduces a time-dependence in the counting efficiency which directly
affects the measured lifetime.
The probability p(t) that a single muon decays per unit of time
after a time t decreases exponentially in time,
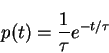 |
(9) |
Therefore, the probability to detect k events in a time span 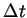 originating from a source containing N muons (with N small) is
governed by the Binomial distribution
originating from a source containing N muons (with N small) is
governed by the Binomial distribution
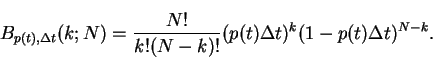 |
(10) |
Here it is tacitly assumed that 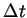 is small enough so that
is small enough so that
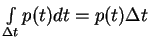 .
In the case that
multiple events during
.
In the case that
multiple events during 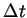 cannot be distinguished by the
experimental apparatus, only one event is counted instead of k. The
average number of events counted in a time window
cannot be distinguished by the
experimental apparatus, only one event is counted instead of k. The
average number of events counted in a time window 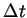 at time
t,
at time
t, 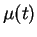 ,
must be modified from
,
must be modified from
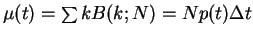 to
to
![\begin{displaymath}
\begin{array}{rl}
\mu(t) & = \sum\limits_{k=1}^{\infty} B(...
...(N-1)\Delta t}{2\tau} e^{-t/\tau} + \dots \right],
\end{array}\end{displaymath}](img88.gif) |
(11) |
i.e a deviation from the pure exponential shape is introduced.
To reduce this deviation, the event separating power can be improved
trivially by segmenting the detector. Additionally, event separating
power can be obtained from information on the signal amplitudes and
the pulse shapes from the detector elements. The magnitude of the
deviation, i.e. the second term between square brackets, is then
reduced by a factor FsegFdh. The factor Fseg is equal to
180 and represents the number of tile segments. The factor Fdh
quantifies the double-hit identification power and is based on pulse
height discrimination in the two scintillator layers. We have
performed GEANT simulations of the tile system using positrons with
energies following the Michel spectrum. For positrons above the
threshold of approximately 2 MeV, the energy deposition profile
corresponds to a typical MIP from the cosmic ray tests. The
simulation has been used to estimate the probability that a single
particle yields a light level in both scintillator layers
corresponding to 2 MIPs. This probability is found to 0.5%,
corresponding to a value for Fdh in the above definition of 200.
We have used the very conservative value of Fdh=10 instead to
account for possible complications due to photostatistics, edge
effects, and other resolution dampening processes.
Figure 11 is a plot of the energy deposited in the
inner versus the outer scintillators for one and two positrons passing
through a tile during the same, unresolved, time period. It is very
clear that a comfortable separation exists between one and two MIPs
when using this two-dimensional representation as a basis for a cut.
Figure 11:
Plot of the energy deposited in the inner versus the outer
scintillators for one and two positrons passing through a
tile during the same, unresolved, time period. This GEANT
simulation shows that it is straightforward to use a
two-dimensional cut to identify double hits.
|
|
To first order, the systematic shift in the measured lifetime is
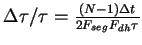 ,
which is
reduced by a factor
,
which is
reduced by a factor 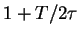 when counts are collected for a
measuring period T. For the design parameters listed in
table 4, a shift of 3 ppm is expected. However,
the parameters determining this shift only need to be known with a
combined accuracy of 30% in order to correct for the shift, which can
be done with relative ease by modeling the level of unobserved pileup.
Pileup is therefore not expected to limit the accuracy of the
measured lifetime.
when counts are collected for a
measuring period T. For the design parameters listed in
table 4, a shift of 3 ppm is expected. However,
the parameters determining this shift only need to be known with a
combined accuracy of 30% in order to correct for the shift, which can
be done with relative ease by modeling the level of unobserved pileup.
Pileup is therefore not expected to limit the accuracy of the
measured lifetime.
Apart from miscounting the number of events, pileup also introduces a
time shift, of which the magnitude is determined by the procedure used
to collect and analyze the data. In a setup in which the decay time
is derived from the time at which the analog signal exceeds a certain
threshold, the unavoidable walk can cause a substantial shift in time.
By using waveform digitizers, this problem is largely eliminated. In
2, we faced and solved a similar problem, and at a much higher
instantaneous rate on the detectors.
Assuming that the detection efficiency does not change during a small
time interval 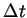 ,
the time associated to a pileup event which
has individually unresolved hits is just the average time of both. As
a result, the distribution of double hit events is shifted by about
15 ps with respect to the distribution of decay times. The effect of
this shift is negligible compared to the effect introduced by the fact
that this distribution has a different shape.
,
the time associated to a pileup event which
has individually unresolved hits is just the average time of both. As
a result, the distribution of double hit events is shifted by about
15 ps with respect to the distribution of decay times. The effect of
this shift is negligible compared to the effect introduced by the fact
that this distribution has a different shape.



Next: Spin Precession
Up: Simulations and Systematic Errors
Previous: Gain and Threshold Stability
Gerco Onderwater
1999-05-25
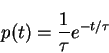
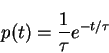
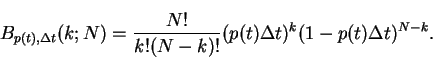
![\begin{displaymath}
\begin{array}{rl}
\mu(t) & = \sum\limits_{k=1}^{\infty} B(...
...(N-1)\Delta t}{2\tau} e^{-t/\tau} + \dots \right],
\end{array}\end{displaymath}](img88.gif)
![\includegraphics*[width=4in]{geantsim}](img89.gif)
![]() ,
which is
reduced by a factor
,
which is
reduced by a factor ![]() when counts are collected for a
measuring period T. For the design parameters listed in
table 4, a shift of 3 ppm is expected. However,
the parameters determining this shift only need to be known with a
combined accuracy of 30% in order to correct for the shift, which can
be done with relative ease by modeling the level of unobserved pileup.
Pileup is therefore not expected to limit the accuracy of the
measured lifetime.
when counts are collected for a
measuring period T. For the design parameters listed in
table 4, a shift of 3 ppm is expected. However,
the parameters determining this shift only need to be known with a
combined accuracy of 30% in order to correct for the shift, which can
be done with relative ease by modeling the level of unobserved pileup.
Pileup is therefore not expected to limit the accuracy of the
measured lifetime.
![]() ,
the time associated to a pileup event which
has individually unresolved hits is just the average time of both. As
a result, the distribution of double hit events is shifted by about
15 ps with respect to the distribution of decay times. The effect of
this shift is negligible compared to the effect introduced by the fact
that this distribution has a different shape.
,
the time associated to a pileup event which
has individually unresolved hits is just the average time of both. As
a result, the distribution of double hit events is shifted by about
15 ps with respect to the distribution of decay times. The effect of
this shift is negligible compared to the effect introduced by the fact
that this distribution has a different shape.