The average instantaneous rate is typically greater at early compared to late times, and this would be the primary source of gain shifts over the course of a measuring period. The maximum rate at the beginning of the measuring period is approximately 23 kHz which is not high for a PMT-scintillator system. The average rate is approximately 4 kHz. Rate becomes an issue if two particles strike the same tile in the same measuring period. The probability for this to occur is quite low, (.04)2 = 0.0016, and if necessary can be corrected for if time shifts are noted. Just after injection, we might have to deal with a slight "flash" in the forward tiles due to positrons and perhaps other sources. The positron contamination in the PSI beamlines is expected to be only a few percent and thus poses no major problem. The effect we will watch carefully is whether any time shifts occur in a PMT/base/WFD system due to a recent firing of the same detector.
The detection efficiency can change due to two causes:
The fraction of events stopping in the second layer can easily be
evaluated using the theoretical energy distribution n(y) as given
above and the fractional energy loss dE/dx for electrons from
standard tables. Using this, the fraction of positrons stopping in
the outer scintillator layer has been calculated for thicknesses of
both layers varying from 1 mm to 20 mm and found to range up to about
0.08%. The stopping fraction depends more strongly on the thickness
of the outer layer than on that of the inner layer, which suggests
that the outer layer should be thinner than the inner one. For the
selected thicknesses of 6.35 and 3.17 mm for the inner and outer
layer, respectively, the fraction of stopped positrons is
![]() .
The quantity
.
The quantity ![]() is the detection threshold in
units of the energy deposited by a MIP. Assuming a uniform energy
distribution for stopping positrons, this implies that a change in the
threshold
is the detection threshold in
units of the energy deposited by a MIP. Assuming a uniform energy
distribution for stopping positrons, this implies that a change in the
threshold ![]() corresponds to a change in the fraction of
stopped positrons we detect of
corresponds to a change in the fraction of
stopped positrons we detect of
![]() .
For
small times, when drifting is expected to be most severe, the relative
change in the measured lifetime is proportional to the relative change
in the number of events. Therefore, the stability of the threshold
.
For
small times, when drifting is expected to be most severe, the relative
change in the measured lifetime is proportional to the relative change
in the number of events. Therefore, the stability of the threshold
![]() needs to be controlled to within 1.0%, which is certainly
feasible.
needs to be controlled to within 1.0%, which is certainly
feasible.
The fraction of events that do not stop in the second layer, but
nonetheless produce a signal below threshold, depends on statistical
fluctuations in the number of photoelectrons. For a large enough
number of photoelectrons Gaussian statistics can be assumed, so that
![]() ,
with NMIP the average number
of photoelectrons produced by a minimum ionizing particle. Ignoring
the Landau tail of the energy deposited in the scintillator, the
fraction of events below threshold is
,
with NMIP the average number
of photoelectrons produced by a minimum ionizing particle. Ignoring
the Landau tail of the energy deposited in the scintillator, the
fraction of events below threshold is
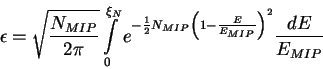 |
(8) |