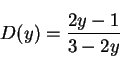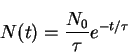Next: Gain and Threshold Stability
Up: Proposal for: A Precision
Previous: Beamtime Estimate
We have made a preliminary study of a number of potential sources of
systematic error in a measurement of the muon lifetime. We want to
reduce the uncertainty on the muon lifetime to the 1 ppm level, which
implies an absolute precision of about 2.2 ps per lifetime. The term
absolute precision implies that the average measured times must be
stable to a precision of 2.2 ps.
Any systematic problem with the experimental apparatus which causes a
deviation from a pure exponential shape in the data can lead to an
error in the measured muon lifetime. Deviations from one decay period
to the next are generally much less dangerous than deviations within a
given period. In particular, we must be vigilant for shifts in timing
or pulse heights at early times (at the beginning of the measuring
period, just after muon injection) compared to late times (at the end
of the measuring period, many lifetimes after the muon injection) in a
given cycle. Some of the more important error sources are:
- 1.
- Gain and threshold instability;
- 2.
- Pileup;
- 3.
- Counting asymmetries due to spin precession;
- 4.
- Rare decay modes;
- 5.
- Cosmic rays and beam related backgrounds.
In the sections which follow, we examine each of these items in turn
and make estimates based on simulations which indicate that these
systematic errors are less than the proposed statistical uncertainty.
The parameters given in table 4 are typical input
values to the simulations. An overarching aspect of these studies is
the distribution of positron energies and angles according to the
Michel spectrum:
![\begin{displaymath}
\frac{dP(y,\alpha)}{dy\,d\Omega} = n(y)\left[1+D(y)\cos\alpha \right]
\end{displaymath}](img64.gif) |
(3) |
with
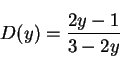 |
(5) |
for 100% polarized muons and
where pe,max is the maximum momentum of the decay positron in the
center of mass frame of the muon. The angle 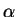 is the angle
between the momentum of the decay positron and the muon spin.
is the angle
between the momentum of the decay positron and the muon spin.
The rate of events at a given time is
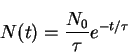 |
(7) |
Table 4:
Parameters used in the design of the experiment and their typical values.
Symbols for selected variables as discussed in the next section.
| Quantity |
Symbol |
Typical value |
| experimental goal ppm |
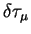 |
1 ppm |
| required number of events |
|
1012 |
| muon lifetime |
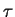 |
2197.03 ns |
| accumulation period |
Tacc |
1 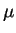 s s |
| measuring period |
T |
11 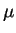 s s |
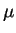 's at T0 's at T0 |
N0 |
12 |
| geometrical acceptance |
|
75% |
| detector segmentation |
Fseg |
180 |
| average rate per tile |
|
4.1 kHz |
| maximum rate per tile |
|
22.7 kHz |
| time resolving power |
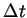 |
10 ns |
| double-hit identification |
Fdh |
10 |
| external magnetic field |
B |
75 G |
| spin precession frequency |
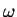 |
1 MHz |
| fractional energy |
y |
0 - 1 |
| detection threshold |
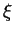 |
0.04 |
| spin modulation amplitude |
D |
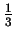 - 1
- 1 |



Next: Gain and Threshold Stability
Up: Proposal for: A Precision
Previous: Beamtime Estimate
Gerco Onderwater
1999-05-25
![\begin{displaymath}
\frac{dP(y,\alpha)}{dy\,d\Omega} = n(y)\left[1+D(y)\cos\alpha \right]
\end{displaymath}](img64.gif)
![\begin{displaymath}
\frac{dP(y,\alpha)}{dy\,d\Omega} = n(y)\left[1+D(y)\cos\alpha \right]
\end{displaymath}](img64.gif)