The surface muons arrive at the target highly polarized with their
spin anti-parallel to their momentum direction. If some net average
polarization S remains after the muons have stopped in the target,
then the spin will precess with angular frequency ![]() along an
axis parallel to any existing magnetic field B. The precession
frequency is proportional to B and to the muon's g-factor. For a
free muon, the precession rate
along an
axis parallel to any existing magnetic field B. The precession
frequency is proportional to B and to the muon's g-factor. For a
free muon, the precession rate
![]() rad/sT,
which corresponds to a revolution frequency of 13.5 kHz per gauss. In
the case of free muonium, i.e. a muon bound to an electron, in a
spin-triplet state, the precession rate is much larger,
rad/sT,
which corresponds to a revolution frequency of 13.5 kHz per gauss. In
the case of free muonium, i.e. a muon bound to an electron, in a
spin-triplet state, the precession rate is much larger,
![]() rad/sT. However, we do not expect muonium to form
at any appreciable level in the stopping target we will use and, as
outlined below, faster precession is better.
rad/sT. However, we do not expect muonium to form
at any appreciable level in the stopping target we will use and, as
outlined below, faster precession is better.
If S and ![]() are both non-zero, the precession of the muon
spins will produce a change in the angular distribution of the decay
positrons, and, consequently, a change with time of the number of
counts registered in any element of a segmented detector. This
precession will alter the expected pure exponential shape of the decay
and is therefore a potential source of systematic error. The detector
asymmetry, magnetic field, and residual muon polarization can never be
guaranteed to vanish individually at the ppm level. To understand how
spin precession affects the extraction of
are both non-zero, the precession of the muon
spins will produce a change in the angular distribution of the decay
positrons, and, consequently, a change with time of the number of
counts registered in any element of a segmented detector. This
precession will alter the expected pure exponential shape of the decay
and is therefore a potential source of systematic error. The detector
asymmetry, magnetic field, and residual muon polarization can never be
guaranteed to vanish individually at the ppm level. To understand how
spin precession affects the extraction of ![]() ,
we divide the
contribution according to the three major items which will influence
the result. They are:
,
we divide the
contribution according to the three major items which will influence
the result. They are:
With respect to a fixed orientation of the muon spin, the detector can
be expected to be asymmetric due to alignment, energy acceptance i.e. threshold and intrinsic efficiency. All of these are ultimately
related to the angular and energy distribution of the decay positrons;
both depend on the angle ![]() between the momentum of the decay
positron and the muon spin. With a threshold at
between the momentum of the decay
positron and the muon spin. With a threshold at ![]() and an
average remnant polarization of the muons with value S, the detected
fraction of events
and an
average remnant polarization of the muons with value S, the detected
fraction of events
![]() is
is
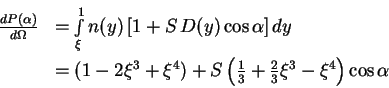 |
(12) |
For the lifetime analysis, consider the sum of the two tile
pairs as a single counter. The individual tiles in this pair are
defined to have overall geometrical and intrinsic efficiencies of
![]() and
and
![]() .
Considering their
respective thresholds separately as energy-dependent differences
introduces the additional factors of
.
Considering their
respective thresholds separately as energy-dependent differences
introduces the additional factors of ![]() and
and
![]() .
For a non-zero magnetic field, a small
modulation will be observed whose amplitude A is given by
.
For a non-zero magnetic field, a small
modulation will be observed whose amplitude A is given by
![\begin{displaymath}
A = S\left[
\frac{1}{3}\left(\eta_\alpha - \eta_{\overline...
..._{\overline{\alpha}}\xi_{\overline{\alpha}}^4 \right)
\right]
\end{displaymath}](img102.gif) |
(13) |
A typical value for the detection threshold is 2 MeV corresponding to
![]() = 0.04. The first term on the right hand side therefore
dominates the amplitude, i.e.
= 0.04. The first term on the right hand side therefore
dominates the amplitude, i.e.
![]() .
This states that it is
important to keep the geometric and intrinsic differences small
between the pairs of tiles. Integrated over the whole detector, the
intrinsic efficiency component in this term will largely vanish.
However, a global alignment asymmetry can certainly be expected.
Therefore, we take the value for the detector-related dilution of the
asymmetry to be no smaller than
.
This states that it is
important to keep the geometric and intrinsic differences small
between the pairs of tiles. Integrated over the whole detector, the
intrinsic efficiency component in this term will largely vanish.
However, a global alignment asymmetry can certainly be expected.
Therefore, we take the value for the detector-related dilution of the
asymmetry to be no smaller than
![]() .
.
Muons enter the target with nearly 100% polarization. The use of a sulfur target is known to depolarize the muons during the stopping phase to a level below approximately 3%. Using this figure, the residual polarization average for a single muon, at the time of stopping, has the value <S> = 0.03.
At PSI, the ``pulsed'' beam will be made by simply chopping out
approximately 90% of the beam. The 10% accumulation period should
have no structure in the rate of incoming muons. Therefore, muons
arriving early in this period will have precessed more than those
arriving late. This implies that the muon spins will be automatically
dephased with respect to one another, depending on the size and
direction of an external magnetic field. For a sample of muons
stopped in the target with their spin vectors initially aligned
antiparallel to the beam direction, the residual ensemble-averaged
polarization at the end of the accumulation period is ![]() .
For
example, a field strength which precesses the spin by
.
For
example, a field strength which precesses the spin by ![]() during a
full accumulation period results in a depolarized distribution, i.e.,
during a
full accumulation period results in a depolarized distribution, i.e.,
![]() .
The cancellation of the asymmetry will not be complete
because some of the earliest arriving muons decay. A plot of
.
The cancellation of the asymmetry will not be complete
because some of the earliest arriving muons decay. A plot of ![]() versus the length of the accumulation period, Tacc, is shown in
figure 12 for a magnetic field strength of 75 G. It
has minima when the product of the magnetic field and the accumulation
period combine to rotate the muon spin in integer multiples of
versus the length of the accumulation period, Tacc, is shown in
figure 12 for a magnetic field strength of 75 G. It
has minima when the product of the magnetic field and the accumulation
period combine to rotate the muon spin in integer multiples of ![]() .
At this field, the first minimum occurs for a
.
At this field, the first minimum occurs for a ![]() accumulation
period. We have tested small permanent rare-earth magnets which are
capable of making such a field easily over the area of the disk-like
target. Figure 13 illustrates the effect for a
series of 15 muons arriving during the accumulation period of
accumulation
period. We have tested small permanent rare-earth magnets which are
capable of making such a field easily over the area of the disk-like
target. Figure 13 illustrates the effect for a
series of 15 muons arriving during the accumulation period of ![]() and a B field of 75 G. The average polarization of the ensemble
is shown as the dark line in the figure and remains close to zero
during the measuring period.
and a B field of 75 G. The average polarization of the ensemble
is shown as the dark line in the figure and remains close to zero
during the measuring period.
![\includegraphics*[width=4in]{dephase}](img109.gif)
|
![\includegraphics*[width=4in]{dephasing}](img110.gif)
|
Taken together, the detector symmetry, the depolarization during
stopping and the dephasing reduces the influence on ![]() well
below the necessary 1 ppm level. Figure 14 shows the
shift in the measured
well
below the necessary 1 ppm level. Figure 14 shows the
shift in the measured ![]() versus applied external magnetic
field for a series of simulations which progressively includes the
factors discussed above. The top curve corresponds to a single muon,
a single counting tile, and a non-depolarizing target. Next the
summed response from a diametrically opposed tile pair is used
assuming the tile pair efficiency is matched to no better than 2%.
The next curve adds in the depolarization effect due to the use of a
sulfur target and the final curve includes the dephasing process. We
have used relatively conservative factors in this simulation. For a
magnetic field near 75 G, the shift in
versus applied external magnetic
field for a series of simulations which progressively includes the
factors discussed above. The top curve corresponds to a single muon,
a single counting tile, and a non-depolarizing target. Next the
summed response from a diametrically opposed tile pair is used
assuming the tile pair efficiency is matched to no better than 2%.
The next curve adds in the depolarization effect due to the use of a
sulfur target and the final curve includes the dephasing process. We
have used relatively conservative factors in this simulation. For a
magnetic field near 75 G, the shift in ![]() is a few tenths of
a ppm.
is a few tenths of
a ppm.
![\includegraphics*[width=4in]{suppress}](img111.gif)
|