One of the great triumphs of high-energy physics in the last decade is
the impressive agreement between theoretical predictions of the
Standard Model of electroweak interactions and experiments performed
at LEP, SLC and elsewhere. Most spectacular was the accuracy of the
prediction for the mass of the top quark before it had been directly
measured at FNAL. This prediction took the measured value for the
Fermi coupling constant, GF, along with ![]() and MZ, as
starting points and obtained a value for the top quark mass by fitting
to electroweak data. The value obtained by this method is
and MZ, as
starting points and obtained a value for the top quark mass by fitting
to electroweak data. The value obtained by this method is
![]() GeV [5] to be compared with the current CDF
and D0 average of
GeV [5] to be compared with the current CDF
and D0 average of ![]() GeV. Indeed it is input from the
charged-current sector of the theory, coming solely from GF, that
is the source of a quadratic sensitivity to the top quark mass and
therefore drives the prediction [6]. The value of GF, in
turn, is best determined from the muon lifetime where it is often
termed
GeV. Indeed it is input from the
charged-current sector of the theory, coming solely from GF, that
is the source of a quadratic sensitivity to the top quark mass and
therefore drives the prediction [6]. The value of GF, in
turn, is best determined from the muon lifetime where it is often
termed ![]() .
The relationship is
.
The relationship is
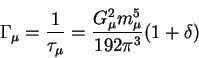 |
(1) |
For many years, the errors on ![]() and GF were negligible
compared to that of MZ. Now the situation has changed and the
error on MZ is 1.8 MeV, or about 2 parts in 105, which is
comparable to that of
and GF were negligible
compared to that of MZ. Now the situation has changed and the
error on MZ is 1.8 MeV, or about 2 parts in 105, which is
comparable to that of ![]() .
As Stuart and von Ritbergen point out
in their recent definitive paper [1] on the relation between
the Fermi coupling constant and the muon lifetime, the expected error
on the Z mass measurement at LEP was an order of magnitude larger than
that which was ultimately achieved. Indeed, measurements at a muon
collider may well improve our knowledge of the Z mass by another order
of magnitude. It therefore makes sense to improve the measurement of
.
As Stuart and von Ritbergen point out
in their recent definitive paper [1] on the relation between
the Fermi coupling constant and the muon lifetime, the expected error
on the Z mass measurement at LEP was an order of magnitude larger than
that which was ultimately achieved. Indeed, measurements at a muon
collider may well improve our knowledge of the Z mass by another order
of magnitude. It therefore makes sense to improve the measurement of
![]() to the extent that current facilities and technology allow,
and to the extent that current theoretical understanding permits us to
interpret the result.
to the extent that current facilities and technology allow,
and to the extent that current theoretical understanding permits us to
interpret the result.
Until recently, the relative error on the Fermi constant of
1.7 x 10-5 was dominated by a theoretical error of
1.5 x 10-5, which was an estimate of unknown 2-loop QED
corrections in the ![]() term above. In their most recent
paper [1], von Ritbergen and Stuart published results for
the unknown corrections as well as confirmation of terms that had
already been calculated by other authors. Completion of the 2-loop
QED corrections required the calculation of matrix elements for the
processes
term above. In their most recent
paper [1], von Ritbergen and Stuart published results for
the unknown corrections as well as confirmation of terms that had
already been calculated by other authors. Completion of the 2-loop
QED corrections required the calculation of matrix elements for the
processes
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
with up to 2
virtual photons. The corrections are dominated by Feynman diagrams of
two kinds: those which purely are photonic, containing no
charged-fermion loops, and diagrams containing an electron loop or
e+ e- pairs in the final state. Diagrams involving muon loops and
virtual hadrons are several orders of magnitude smaller. Overall, the
residual theoretical uncertainty arising from missing higher order QED
corrections are no larger than a few tenths of a ppm and thus the
theoretical uncertainty on the extraction of the Fermi constant has
been entirely eliminated (see also [7] and [8]).
,
with up to 2
virtual photons. The corrections are dominated by Feynman diagrams of
two kinds: those which purely are photonic, containing no
charged-fermion loops, and diagrams containing an electron loop or
e+ e- pairs in the final state. Diagrams involving muon loops and
virtual hadrons are several orders of magnitude smaller. Overall, the
residual theoretical uncertainty arising from missing higher order QED
corrections are no larger than a few tenths of a ppm and thus the
theoretical uncertainty on the extraction of the Fermi constant has
been entirely eliminated (see also [7] and [8]).
Stuart and von Ritbergen also discuss the electroweak corrections to
muon decay, which can be separated in a natural way from those
involving QED alone. The electroweak corrections are contained in the
term ![]() ,
where the equation
,
where the equation
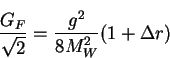 |
(2) |
The importance of GF does not end with the top quark mass
prediction. Now that the top quark mass has been directly measured
and incorporated into the Standard Model, our knowledge of GF
will ultimately help in understanding in detail, the Higgs sector,
through its radiative corrections. GF is also very useful in
analyzing extensions to the Standard Model as discussed recently by
Marciano [9]. It is the input from GF, through the
![]() -parameter, that is responsible for the strongest constraints on
sparticle mass splittings in SUSY models. But in the end, we simply
do not know what arrangements have been made by nature, and it is our
belief that the measurement of fundamental constants, that can be
performed with great precision, will be of enduring value.
-parameter, that is responsible for the strongest constraints on
sparticle mass splittings in SUSY models. But in the end, we simply
do not know what arrangements have been made by nature, and it is our
belief that the measurement of fundamental constants, that can be
performed with great precision, will be of enduring value.