diffusion.nb

Setup

Analytical formulation

1/r^2 (Csc[theta]^2 f^(0, 0, 2)[r, theta, phi] + Cot[theta] f^(0, 1, 0)[r, theta, phi] + f^(0, 2, 0)[r, theta, phi] + 2 r f^(1, 0, 0)[r, theta, phi]) + f^(2, 0, 0)[r, theta, phi]

Gaussian kernel gives solution with u(r,0)=delta(r), lim u(r,t)->0 (r-∞). a=2 c t. In addition a loss term is included. Spherical symmetric solution in r.

$c=. ; d=. ; G[a_, d_] := (2 π a)^-3/2 Exp[-r^2/(2 a)] Exp[-d t] g = G[2 c t, d] d1 = Simpli ... r] + D[g, {r, 2}]] - d g d3 = c FullSimplify[1/r^2 D[r^2 D[g, r], r]] - d g FullSimplify[d1 - d2]$

e^(-r^2/(4 c t) - d t)/(8 π^(3/2) (c t)^(3/2))

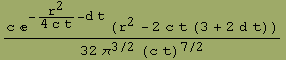
(c e^(-r^2/(4 c t) - d t) (r^2 - 2 c t (3 + 2 d t)))/(32 π^(3/2) (c t)^(7/2))

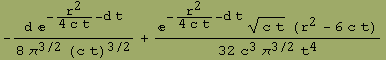
-(d e^(-r^2/(4 c t) - d t))/(8 π^(3/2) (c t)^(3/2)) + (e^(-r^2/(4 c t) - d t) (c t)^(1/2) (r^2 - 6 c t))/(32 c^3 π^(3/2) t^4)

-(d e^(-r^2/(4 c t) - d t))/(8 π^(3/2) (c t)^(3/2)) + (e^(-r^2/(4 c t) - d t) (c t)^(1/2) (r^2 - 6 c t))/(32 c^3 π^(3/2) t^4)

f[r_, t_, d_] := e^(-r^2/(4 c t) - d t)/(8 π^(3/2) (c t)^(3/2)) f[r, t, d]

e^(-r^2/(4 c t) - d t)/(8 π^(3/2) (c t)^(3/2))

[Graphics:diff_files/diffusion_17.gif]

[Graphics:diff_files/diffusion_18.gif]

Numerical estimates

Following Valery's equations at the end of our original proposal we get (sigma is tranport cross section)

DK[l_, v_] := (v l)/3 l[sig_] := 1/(2^(1/2) sig NH) R[t0_] := (v t0)/(sig NH)^(1/2)

Plug in numbers (cm units)

$NH = 4.25 10^22 0.01 0.5 sig = 2.08 10^(-19) v = 0.26 {R[1], R[2.2]}$

Created by Mathematica (August 18, 2005)